Next, we reviewed superposition in ac circuits. It is very similar to superposition in dc, with the exception that impedance is used and therefore complex algebra, as in the other analysis techniques in ac. Lastly, source transformations and Thevenin and Norton equivalents were also reviewed, which involve the same concepts as in dc but the same exceptions as in the other analysis techniques in ac.
LECTURE:
In this problem, nodal analysis was used in ac circuits to find the current across the 0.1 uF capacitor. There are only two viable voltage nodes, which were used for the analysis.
In this problem, the objective was to find the current across the 4 ohm resistor. This was achieved using mesh current analysis, and again, because we are in ac, more complex algebra was seen.
In this problem, superposition principle was used to find the current across the 4 ohm resistor. As can be seen, this is the same circuit that was analyzed in the previous example. The same circuit was used to verify that superposition principle and mesh analysis can be used in ac circuits correctly. The same conditions apply for superposition in ac as in dc; current sources act as open circuits and voltage sources act as short circuits.
In this simple problem, source transformations were practiced in simple ac circuit analysis. They ae performed the same exact way as in dc circuit analysis, with the exception that now complex algebra must be used.
The Thevenin equivalent of this circuit was determined using Thevenin's Theorem and impedance equivalents. The pair of impedances in series were added to obtain equivalent impedances, and then KCL and KVL was performed to solve for the Thevenin voltage and Thevenin impedance.
LAB:
Purpose:
The purpose of this experiment was to analyze the steady-state response of an RL circuit with AC signals applied. The frequency was the same throughout the entire circuit, but each component had a different phase angle and amplitude. Because they are all at the same frequency as well, the amplitude gain between the input and output could be determined. The experimental values were confirmed by comparing to theoretical values solved for in the prelab.
Prelab:
In the prelab, the amplitude gain and phase difference were derived for an RL circuit. Then the cutoff frequency of this circuit was solved for with the given resistance and capacitance values. The cutoff frequency is R/L for an RL circuit. Next, the amplitude gain and phase difference at a tenth of the cutoff frequency, at the cutoff frequency, and at ten times the cutoff frequency were calculated. Then, the behavior of the inductor at those frequencies was predicted and used to prove the calculated amplitude gain. At low frequencies, the inductor acts close to a wire, providing a very large amplitude gain. On the other hand, at high frequencies, the inductor acts close to an open cicuit, providing a very small amplitude gain.
Apparatus:
The equipment of this experiment included: a breadboard, an inductor, a resistor, wires, an analog discovery and a laptop with Waveforms.
Procedure:
First, the RL circuit, consisting of a 47 ohm resistor in series with a 1 mH inductor, was created. Then, the wavegen on waveforms was used to apply a sinusoidal input of 2 V at the frequencies given by a tenth of the cutoff frequency, the cutoff frequency itself, and ten times the cutoff frequency. Channel 1 was used to measure the input voltage, and channel two of the oscilloscope was used to measure the voltage across the inductor. Then, a math channel was used to determine the current through the circuit. The formula is shown below:
Below is the oscilloscope window for a tenth of the cutoff frequency:
As can be seen, the voltage across the inductor is very small, which shows that it acts close to a wire under low frequencies. The oscilloscope window for the cutoff frequency is shown below:
Lastly, the oscilloscope window for 10 times the cutoff frequency is shown below:
As can be seen, the voltage across the inductor is roughly equal to the input voltage, which shows that at high frequencies it acts like an open circuit, eating up almost all of the voltage provided.
All of the data obtained form analyzing the windows is shown in data below:
Data:
Above is the data obtained from the oscilloscope windows. Again, it is expected that the voltage drop across the inductor at low frequencies is small, because the inductor acts close to a wire. At high frequencies, it is expected that the inductor eats up nearly all of the voltage applied, since it acts as an open circuit at high frequencies. Therefore, it is also expected that the current is very small at these high frequencies.
Data Analysis/Conclusion:
Analyzing the data obtained to the calculations in the prelab, all of the obtained data is very close to the calculated values, which shows that the circuit analysis used in this experiment is correct. It is expected that the gain at low frequency is the largest and the gain at high frequency is the smallest, since at low frequencies the inductor acts as a wire and at high frequencies the inductor acts as an open circuit. In addition, the phase shifts obtained experimentally are very close to the determined values, which shows that the analysis is correct. Unfortunately, there is no conceptual way to determine the phase shift at the frequencies as there is for the gain and current.







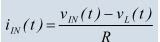




jmz,zj z
ReplyDelete