LECTURE:
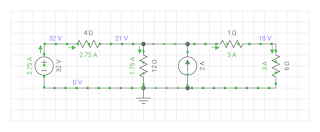
We first did more practice using Every Circuit by building the circuit below in the application and finding the current across the 6 ohm resistor.
We then learned about Thevenin's Theorem, which allows us to simplify any linear circuit across a load (usually a resistor) to a voltage source and resistor in series. This voltage source is called the Thevenin voltage and the resistor is called the Thevenin resistance. The Thevenin resistance is obtained by setting all independent current and independent voltage sources to zero (i.e. voltage sources become wires and current sources become open circuits). The resistors left in the circuit are then added to find the equivalent resistance, which turns out to become the Thevenin resistance.
To find the Thevenin voltage, the different techniques learned, such as node voltage method, mesh current method, superposition and source transformations can be used to find the voltage across the load of interest. The load is also removed from the circuit while measuring both the Thevenin voltage and resistance.
The schematic of the circuit above was then applied to Thevenin's Theorem to find the current across the 6 ohm resistor. This is seen below:
The Thevenin voltage was found to be 30 V and the Thevenin resistance was found to be 4 ohms. In the new circuit, the Thevenin voltage source, the Thevenin resistor and the load resistor are in series. Dividing the Thevenin voltage by the equivalent resistance (4 + 6 = 10 ohms) it can be seen that the current across the 6 ohm resistor was also found to be 3 A using Thevenin equivalents.
In another problem, the same objective as the previous problem, to find the current across the load resistor, was achieved by using Thevenin's Theorem. In this case, the current as a function of the resistance value of the load resistor was obtained. It was found that the Thevenin resistance was 10 ohms and the Thevenin voltage was 40 V. Redrawing the Thevenin circuit, we get the 40 V Thevenin power supply connected to the 10 ohm Thevenin resistance and the load resistor.
Doing so we get the function of the current across the load resistor as a function of the resistance to be the Thevenin voltage divided by the equivalent resistance, or:
Then, the problem asked us to solve for the current running through the load resistor when it has various resistance values. This is done by just substituting the value into R_L in the current equation and simplifying.
We were then supposed to learn about Norton's Theorem, which is, simply putting, the idea of using source transformations in Thevenin equivalents. However, we were barely able to scratch the surface of Norton's Theorem due to an unexpected emergency drill performed by Mt. SAC in our building.
LAB:
Thevenin's Theorem:
Purpose:
The purpose of this experiment was to determine experimentally the validity of Thevenin's Theorem in linear circuits. This was achieved by taking a provided circuit, finding the Thevenin equivalents of voltage and resistance across a load resistor R, then measuring the load voltage across R in the original circuit and the created Thevenin equivalents circuit and comparing the two values, which ideally should be nearly equal if Thevenin's Theorem holds to be true.
In addition, the power dissipated in the load resistor R as a function of load resistance was found by using a potentiometer, which is a variable resistor. The voltages at different resistances was obtained, and a graph was created using that data.
Prelab:
The circuit in the above schematic was the circuit used in this experiment. As seen, the circuit was first created in Every Circuit for extra practice, and to determine the voltage across the load resistor (which was given a value of 6.8k ohms) to compare with the measured load voltage for validity; the load resistor is the highest resistor in the circuit, in series with the 1k ohm and 1.5k ohm resistors. The load voltage was found to be 0.22 V.
Then, the Thevenin voltage and resistance were calculated as seen below:
The Thevenin resistance was found by turning off all voltage sources and finding the equivalent resistance in the circuit. It was found to be 7.4k ohms. Next, the Thevenin voltage was found by finding the voltages across the 4.7k ohm and 6.8k ohm resistors, then subtracting the two to find the voltage difference across points a and b. The Thevenin voltage was found using mesh current analysis, and was found to be 0.455 V.
Apparatus:
Most of the equipment used in this lab was just the usual equipment used in all circuits labs, and consisted of different resistors, an analog discovery power supply, a breadboard, a laptop with Waveforms software, alligator clips, a DMM and wires. The only unique apparatus used in this experiment was a potentiometer, or a variable resistor. This was used in determining the power as a function of load resistance.
Procedure:
First, the actual resistances of the used resistors was measured using an ohmmeter. Then. the circuit provided in the Every Circuit schematic was built without including the load resistor. The open-circuit voltage across the 1.5k ohm and 1k ohm terminals was then measured using a voltmeter, as seen below:
The Thevenin voltage was measured as 0.448 V. In addition, the Thevenin resistance was also measured by replacing the voltage sources with wires, then connecting the ohmmeter across the terminals a and b (one end of th1 1k ohm and 1.5k ohm resistors), as seen below:
The Thevenin resistance was measured to be 7.36k ohms. Then, a random load resistor with a resistance value between 4k ohs and 10k ohms was integrated into the circuit. A 6.8k ohm resistor was used, just because in Every Circuit a 6.8k ohm resistor was placed as the load resistor. The circuit is shown in the picture below:
The load voltage was measured as 0.212 V. After, the Thevenin equivalent circuit was built, which consisted of a 0.455 V source in series with a bunch of resistors that added to an equivalence of 7.4k ohms. The load resistor used in the previous circuit was then integrated into the Thevenin equivalent circuit, and the voltage across the load resistor R was measured, as seen below:
Thevenin circuit sketch
The load voltage in the Thevenin circuit was measured to be 0.209 V, which is lower than expected due to the higher Thevenin resistance of 7.59k ohms. Lastly, the load resistor was replaced with a potentiometer in the original circuit. Its resistance was changed constantly so that the load voltage could be measured as a function of the load resistance. These data points were then used to find the power of the potentiometer as a function of the load resistance, using the formula for the power of a resistor due to voltage, or P = (V*V)/R. The setup is found below:
Data Analysis and Conclusion:
Seen above is all of the data measured in this experiment, such as resistance values, load voltages, Thevenin voltages and Thevenin resistances.
The Thevenin resistance was measured to be 7.36k ohms, which is very close to the theoretical of 7.4k ohms (a percent error of -0.54%). The open circuit voltage was also measured to be 0.448 V, which is also very close to the theoretical value of 0.455 V (a percent error of -1.54%).
The voltage across the load resistor was found to be 0.212 V. Based on the Every Circuit schematic the true voltage was found to be 0.22 V, which is close to the measured value (a percent error of -3.64%).
The voltage across the load resistor in the Thevenin equivalent circuit was found to be 0.209 V, which is still fairly close to the expected value of 0.22 V (a percent difference of -5.0%). The reason it is a little off is due to the higher resistance in the Thevenin circuit.
Below is the data of resistance versus voltage for the potentiometer measurements.
As the resistance increased, the voltage decreased, which is expected. Below is the data for the power versus resistance for the potentiometer and the graph which shows the equation of this relationship.
The maximum power theorem states that the max power in the load resistor is reached when its resistance is equal to that of the Thevenin resistance. Therefore, it was found that the max power drawn by the load resistor occurs when it is 7.4 kOhms, and the max power is:
It seems that our data is significantly off. This is due to the potentiometer being hard to integrate into the circuit and to measure the exact resistance. The difficult of using the potentiometer is what threw off our data. If actual resistors were used our data would become much more accurate; it was just difficult to predict so when we never learned about the maximum power transfer theorem prior to this experiment.
Summary:
In class we first learned about Thevenin's theorem. We then did more practice in Every Circuit and used Thevenin's Theorem in two problems. After, we did the Thevenin's Theorem lab and created a Thevenin equivalent circuit. Lastly, we scratched the surface of Norton's Theorem and learned that we will learn more about it next class along with the maximum power theorem.
















No comments:
Post a Comment