Day 11: Operational Amplifiers and Inverting Voltage Amplifier

In class today we learned about operational amplifiers and how to analyze electrical circuits in which they are present in. Under the hood an operational amplifier is very complex, with many resistors, capacitors and transistor in an interconnected network. However, we learned that we can simplify them and treat them as a very large resistor attached across the input terminals and a voltage-controlled voltage source in series with a resistor across the output terminal. The dependent voltage source relies on the voltage across the very large resistor. We then learned that we must take into account which input terminal the voltage source is connected to. If it is attached to the non-inverted terminal, we treat the voltage source as positive, and a positive gain should be obtained. If the voltage source is attached to the inverted terminal, the voltage source is treated as negative, and a negative gain is obtained. We also learned about an open loop versus a closed loop. An open loop results in no feedback between the output and input (i.e. the output and input terminals are not connected). A closed loop, as implied, has feedback between the output and input of the op amp (i.e. the input and output terminals are connected.
After, we did the lab titled "Inverting Voltage Amplifier". Once we finished the lab we then learned about ideal operational amplifiers and how so much simpler they make the circuit. An ideal amplifier has an infinite resistance for the resistor connected across the inverted and non-inverted terminals. This means that no current runs through the resistor and therefore no current through the wires attached to the terminals. No current means no voltage across the resistor; this results in the voltage-controlled voltage source providing no voltage, and therefore means no current running through the output wire of the amplifier. 

LECTURE:

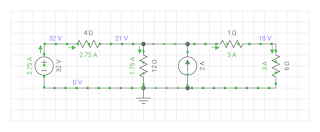
This problem involved an operational amplifier with the voltage source attached to the noninverted terminal. The operational amplifier was redrawn to consist of a resistor attached to the terminals with a potentional difference Vd and on another branch a voltage source dependent on Vd with a resistor in series. The output voltage was found via node-voltage analysis, and the gain of the amplifier was also calculated. 

This problem involved an operational amplifier as well. However, the voltage source was attached to the inverted terminal, resulting in a positive output voltage. Node-voltage analysis was then used again to solve for the output voltage, the gain of the amplifier and the current running through the wire running outside of the output terminal. Again, as with all operational amplifiers, the voltage controlled voltage source is dependent on the potential across the resistor connected to the inverted and non-inverted terminals.

In this problem, the operational amplifier was treated as ideal. This really simplifies the circuit greatly; in this problem it became a simple voltage source and two resistors in series with each other and the voltage source. The current through the 20 kOhm resistor was then found, along with the gain of the amplifier.

LAB:

Inverting Voltage Amplifier:

Purpose:

The objective of this experiment was to test the gain of the operational amplifier experimentally by seeing the output voltage change when the input voltage was changed. The saturation points for the operational amplifier were also found. Because the voltage is connected to the inverted terminal, it is expected that the gain will be negative.

Prelab:

In this prelab the resistance of resistor R2 was found, and the relationship between the output and input voltages (i.e. the gain) was also found in terms of the resistors. The gain was mathematically found to be -2.

Apparatus:

The equipment used in this experiment consisted of the following pieces: an OP27 operational amplifier, an analog discovery toolbox, a laptop with Waveforms software, resistors, a breadboard, a digital multimeter, wires and alligator clips.

Procedure:

The schematic of the circuit seen in the prelab above was created, as shown in the above picture. The circuit is zoomed in to show more detail, as seen below:

In this circuit, the + 5 V and - 5 V sources (provided by the red and white wires, respectively) were attached to terminals 7 and 4 of the operational amplifier, respectively. The two resistors R1 and R2 were both attached to the second terminal on the op amp, which is the inverted input voltage terminal. In addition, the other end of resistor R2 was connected to terminal 6, or the output terminal. The waveform source (yellow wire) was attached to the end of resistor R1 to provide the varying voltages needed. A ground wire was then attached to terminal 3 of the op amp. Lastly, the DMM, acting as a voltmeter, was connected to terminal 6 in parallel with the resistor R2. The other end of the voltmeter was also attached to another ground wire. An ohmmeter was then used to measure the true resistances of the resistor, whose values are shown below:

Data Analysis:

The waveform generator was then used to apply input voltages ranging from -3 V to 4 V to the circuit, in increments of 0.5 V. The output voltages were then measured using the voltmeter and recorded. The data is seen above in the table of output vs input voltages. At -2.5 V and -3 V the op amp reached its upper saturation, and at 2 V and above it reached its lower saturation point. This data was then used to make a graph that represents the model of the op amp used. This graph is shown below:

Conclusion:

The graph obtained was the expected graph, because there were saturation points on both ends of the voltage spectrum. In addition, as seen by the data, when the input voltages were negative the output voltages were positive and vice versa. This shows that the gain of the op amp is negative, which is expected since the voltage source is attached to the inverted terminal. In addition, the output voltage was nearly the negative of the double of the input voltage at each point, with the exception of saturation points; this shows that our gain is -2. This was the calculated and expected gain, which shows that the simplification used for these operational amplifiers is true and correct. Lastly, looking back at the graph, the slope is -2; this shows that the slope is the gain value and that the relationship determined between the output and input voltages via the resistors used (and therefore gain) is accurate.

Day 9: Maximum Power Transfer Theorem and Resistance Measurement

In class we learned about maximum power transfer theorem, which allows us to find the maximum power that a circuit could deliver to a resistor based on thevenin voltage and resistance. In order for a resistor to draw the most power it could out of a circuit, its resistance must equal the thevenin resistance, which was derived in class by taking the partial derivative and setting equal to zero the equation for power as a function of the load resistance. The equation is found below:

From the derivative with respect to load resistance, it was found that thevenin resistance must equal load resistance. Plugging in thevenin resistance for load resistance, we obtain:

Then, we did a problem involving finding max power in a variable resistor. A problem was also done involving applying these concepts to a robotics application to find the internal resistance in a battery. In addition another problem finding the load resistance for max  power in that resistor was done.

We then did a lab on Maximum Power Transfer, which is explained in more detail in the lab section. Lastly, we learned about source modeling and how engineers take into account internal resistance for sources so that the source provides the expected current or voltage. We also did an example on this application. In addition, we learned about a Wheatstone bridge circuit and how it can be used to measure internal resistance via a galvanometer; an example involving this application was performed along with a review problem that puts all of today's concepts together.

LECTURE:

This is the derivation to find the load resistance needed to obtain the maximum power in that resistor. It was done by taking the derivative with respect to the load resistance and setting it to zero since at max power the slope is zero. Again, it was found that the load resistance must equal the Thevenin resistance.

In this problem the Thevenin equivalents were found along with the current through the circuit if the load resistance was 8 ohms. Then, the resistance needed for max power was found (12 ohms) and the power at that resistance was calculated (33.33 W). In addition, power values at different load resistances was found to give us an idea of the curve for power as a function of load resistance.

This problem is the robotics application of max power. The motors in parallel were treated as resistors, and the Thevenin resistance was found. The max power was then found, and using the value that energy needed and amphours used to run this robot was found.

In this simpler problem the load resistance needed to obtain max power was found, which was just using the addition of resistors to find the Thevenin resistance.

In the problem above, the voltage provided to the load resistor was found using source modeling. The above problem shows that a practical source does not actually provide the expected voltage in every circuit it is applied to; it only approaches its expected source values, but only when the load resistance is high enough. If not, it actually provides a lower source value depending on the resistance of the load resistor, as shown above.

In this problem, the resistance needed for R_s in the wheatstone bridge so that no current goes through the galvanometer was found (50 ohms). This type of circuit is used to measure resistance more accurately for medium levels.

Lastly, this problem was just review of the maximum power transfer theorem, along with Thevenin equivalents and source transformations.


LAB:

Maximum Power Transfer:

Purpose:

The purpose of this experiment was to test the max power transfer theorem by setting up a simple circuit with a 5V voltage source, a source resistor of 4.7 kOhms and a variable resistor all in series. The variable resistor was adjusted at resistance values of 1 kOhm to 10 kOhms with an  interval of 1 kOhm, and the power through the resistor at those resistances was found by first measuring the voltage. (NOTE: This lab was performed different than what the lab manual contains; we were proving the maximum power theorem instead of just showing that its conjugate (source resistance equal load resistance) is false).

Apparatus:

The apparatus in this experiment consisted of an analog discovery (5 V source), a source resistor (4.7 kOhm), a potentiometer, a breadboard, a laptop with Waveforms software, a digital multimeter, alligator clips and wires.

Procedure:

The schematic of the circuit in the apparatus section was built as shown below:

The voltages across the potentiometer for each resistance value were then measured with a voltmeter. The resistance in the potentiometer was measured with an ohmmeter. The voltages were then used to calculate the power at each resistance, and the graph below was made using Logger Pro.

The above data was used to make the graph of power versus load resistance below. A model fit was then manually made using the equation for power, which was seen in the introduction.

Data Analysis:

Looking at the graph, it peaks at about 4700 ohms, which is the resistance of our source resistor. This confirms the maximum power theorem, which states that max power is obtained when the load resistance is equal to the source resistance. The equation for the model fit is shown more closely below:

Looking at the equation, A is our thevenin voltage squared, which is 25 volts squared. In the graph, it is in millivolts squared (25000). In addition, B is the source resistance, which is 4700 ohms. The correlation obtained is perfectly 1, which shows our model is an excellent representation of  the maximum power transfer theorem.

3/17/16 Day 8: Every Circuit Practice, Thevenin's Theorem and Norton Equivalents

LECTURE:

We first did more practice using Every Circuit by building the circuit below in the application and finding the current across the 6 ohm resistor.

We then learned about Thevenin's Theorem, which allows us to simplify any linear circuit across a load (usually a resistor) to a voltage source and resistor in series. This voltage source is called the Thevenin voltage and the resistor is called the Thevenin resistance. The Thevenin resistance is obtained by setting all independent current and independent voltage sources to zero (i.e. voltage sources become wires and current sources become open circuits). The resistors left in the circuit are then added to find the equivalent resistance, which turns out to become the Thevenin resistance.

To find the Thevenin voltage, the different techniques learned, such as node voltage method, mesh current method, superposition and source transformations can be used to find the voltage across the load of interest. The load is also removed from the circuit while measuring both the Thevenin voltage and resistance. 

The schematic of the circuit above was then applied to Thevenin's Theorem to find the current across the 6 ohm resistor. This is seen below:

The Thevenin voltage was found to be 30 V and the Thevenin resistance was found to be 4 ohms. In the new circuit, the Thevenin voltage source, the Thevenin resistor and the load resistor are in series. Dividing the Thevenin voltage by the equivalent resistance (4 + 6 = 10 ohms) it can be seen that the current across the 6 ohm resistor was also found to be 3 A using Thevenin equivalents.

In another problem, the same objective as the previous problem, to find the current across the load resistor, was achieved by using Thevenin's Theorem. In this case, the current as a function of the resistance  value of the load resistor was obtained. It was found that the Thevenin resistance was 10 ohms and the Thevenin voltage was 40 V. Redrawing the Thevenin circuit, we get the 40 V Thevenin power supply connected to the 10 ohm Thevenin resistance and the load resistor.

Doing so we get the function of the current across the load resistor as a function of the resistance to be the Thevenin voltage divided by the equivalent resistance, or:

Then, the problem asked us to solve for the current running through the load resistor when it has various resistance values. This is done by just substituting the value into R_L in the current equation and simplifying.

We were then supposed to learn about Norton's Theorem, which is, simply putting, the idea of using source transformations in Thevenin equivalents. However, we were barely able to scratch the surface of Norton's Theorem due to an unexpected emergency drill performed by Mt. SAC in our building.

LAB:

Thevenin's Theorem:

Purpose:

The purpose of this experiment was to determine experimentally the validity of Thevenin's Theorem in linear circuits. This was achieved by taking a provided circuit, finding the Thevenin equivalents of voltage and resistance across a load resistor R, then measuring the load voltage across R in the original circuit and the created Thevenin equivalents circuit and comparing the two values, which ideally should be nearly equal if Thevenin's Theorem holds to be true.

In addition, the power dissipated in the load resistor R as a function of load resistance was found by using a potentiometer, which is a variable resistor. The voltages at different resistances was obtained, and a graph was created using that data.

Prelab:

The circuit in the above schematic was the circuit used in this experiment. As seen, the circuit was first created in Every Circuit for extra practice, and to determine the voltage across the load resistor (which was given a value of 6.8k ohms) to compare with the measured load voltage for validity; the load resistor is the highest resistor in the circuit, in series with the 1k ohm and 1.5k ohm resistors. The load voltage was found to be 0.22 V.

Then, the Thevenin voltage and resistance were calculated as seen below:

The Thevenin resistance was found by turning off all voltage sources and finding the equivalent resistance in the circuit. It was found to be 7.4k ohms. Next, the Thevenin voltage was found by finding the voltages across the 4.7k ohm and 6.8k ohm resistors, then subtracting the two to find the voltage difference across points a and b. The Thevenin voltage was found using mesh current analysis, and was found to be 0.455 V. 

Apparatus:

Most of the equipment used in this lab was just the usual equipment used in all circuits labs, and consisted of different resistors, an analog discovery power supply, a breadboard, a laptop with Waveforms software, alligator clips, a DMM and wires. The only unique apparatus used in this experiment was a potentiometer, or a variable resistor. This was used in determining the power as a function of load resistance.

Procedure:

First, the actual resistances of the used resistors was measured using an ohmmeter. Then. the circuit provided in the Every Circuit schematic was built without including the load resistor. The open-circuit voltage across the 1.5k ohm and 1k ohm terminals was then measured using a voltmeter, as seen below:

The Thevenin voltage was measured as 0.448 V. In addition, the Thevenin resistance was also measured by replacing the voltage sources with wires, then connecting the ohmmeter across the terminals a and b (one end of th1 1k ohm and 1.5k ohm resistors), as seen below:

The Thevenin resistance was measured to be 7.36k ohms. Then, a random load resistor with a resistance value between 4k ohs and 10k ohms was integrated into the circuit. A 6.8k ohm resistor was used, just because in Every Circuit a 6.8k ohm resistor was placed as the load resistor. The circuit is shown in the picture below:

The load voltage was measured as 0.212 V. After, the Thevenin equivalent circuit was built, which consisted of a 0.455 V source in series with a bunch of resistors that added to an equivalence of 7.4k ohms.  The load resistor used in the previous circuit was then integrated into the Thevenin equivalent circuit, and the voltage across the load resistor R was measured, as seen below:

Thevenin circuit sketch

The load voltage in the Thevenin circuit was measured to be 0.209 V, which is lower than expected due to the higher Thevenin resistance of 7.59k ohms. Lastly, the load resistor was replaced with a potentiometer in the original circuit. Its resistance was changed constantly so that the load voltage could be measured as a function of the load resistance. These data points were then used to find the power of the potentiometer as a function of the load resistance, using the formula for the power of a resistor due to voltage, or P = (V*V)/R. The setup is found below:

Data Analysis and Conclusion:

Seen above is all of the data measured in this experiment, such as resistance values, load voltages, Thevenin voltages and Thevenin resistances.

The Thevenin resistance was measured to be 7.36k ohms, which is very close to the theoretical of 7.4k ohms (a percent error of -0.54%). The open circuit voltage was also measured to be 0.448 V, which is also very close to the theoretical value of 0.455 V (a percent error of -1.54%). 

The voltage across the load resistor was found to be 0.212 V. Based on the Every Circuit schematic the true voltage was found to be 0.22 V, which is close to the measured value (a percent error of -3.64%). 

The voltage across the load resistor in the Thevenin equivalent circuit was found to be 0.209 V, which is still fairly close to the expected value of 0.22 V (a percent difference of -5.0%). The reason it is a little off is due to the higher resistance in the Thevenin circuit. 

Below is the data of resistance versus voltage for the potentiometer measurements.

As the resistance increased, the voltage decreased, which is expected. Below is the data for the power versus resistance for the potentiometer and the graph which shows the equation of this relationship.

The maximum power theorem states that the max power in the load resistor is reached when its resistance is equal to that of the Thevenin resistance. Therefore, it was found that the max power drawn by the load resistor occurs when it is 7.4 kOhms, and the max power is:

It seems that our data is significantly off. This is due to the potentiometer being hard to integrate into the circuit and to measure the exact resistance. The difficult of using the potentiometer is what threw off our data. If actual resistors were used our data would become much more accurate; it was just difficult to predict so when we never learned about the maximum power transfer theorem prior to this experiment.

Summary:

In class we first learned about Thevenin's theorem. We then did more practice in Every Circuit and used Thevenin's Theorem in two problems. After, we did the Thevenin's Theorem lab and created a Thevenin equivalent circuit. Lastly, we scratched the surface of Norton's Theorem and learned that we will learn more about it next class along with the maximum power theorem.

3/15/16 Day 7: Superposition (II) and Linearity in Electric Circuits, Time-Varying Signals and Source Transformation

In class today we first did the lab called "Time-varying Signals", where we utilized common voltage functions and analyzed the linear relationship between the functions of the voltage across a circuit element and the voltage across the entire series circuit. After this lab we learned about the linearity of circuits and how it could be useful when solving for currents and/or voltages in linear circuits that are in multiples of each other. Then, a problem using linearity was performed in class. After learning about linearity we learned about superposition in electric circuits, where the current and/or voltage resulting from each voltage and current source can be found seperately, then added together to fnd the true voltage and/or current in the circuit. After, we performed another experiment titled "Superposition II", which involves finding the voltage across a resistor using superposition, then building and testing it to see if superposition in circuits holds true. After the lab we learned about source transformations, where a voltage source can be transformed into an equivalent current source and vice versa depending on the resistance in series to a voltage source or parallel to a current source. This powerful concept was then put to the test in a problem to find the current across a resistor.

LECTURE:

Above is a problem testing the linearity theory of linear circuits. The current Io across the dependent voltage source was found using mesh analysis, when the voltage of the independent source is 24 V. Half of the class solved the problem with Vs being 24 V and the other half with Vs being 12 V. As seen for 24 V, the current Io is 0.32 A. The part of the class using 12 V showed that the current Io is 0.16 A. As can be seen, when the voltage of Vs was doubled the current Io was also doubled, proving the linearity of these circuits.

In this problem, the superposition theory was put to the test. First, the partial current (1 A) across the 5 ohm resistor was found by solely analyzing the 30 V voltage source, making the 6 A current source an open wire. Then, the 6 A current source was only taken into account, leaving the voltage source as a wire. The partial current (2 A) was also solved using this method. Then, the actual current Ix (3 A) across the 5 ohm resistor was found by just summing the partial currents determined using superposition. To test the theory of superposition, this circuit was plugged into EveryCircuit to find the true current value. It was also found to be 3 A, which shows that the theory of superposition is in fact true.

In this last problem, the source transformation analysis was used to determine the current across the 4 ohm resistor adjacent to the 12 V supply. The two current sources were transformed to voltage sources to simplify the circuit. The current through the 4 ohm resistor was found to be 0.111 A.

LAB:

Time-Varying Signals:

Purpose:

The purpose of this experiment was to determine the relationship between the functions of the voltage across a circuit element and the voltage across the entire series circuit. It was found that this relationship is linear; the voltage function across the element is the same, but of a smaller amplitude depending on the ratio of the amount of voltage it uses or provides with the total amount of voltage in the circuit.

Prelab:

The prelab of this experiment was to sketch the voltage functions of a sinusoidal wave, a triangle wave, and a square wave, and to determine the relationship between the voltage as a function of time across a resistor and the total voltage as a function of time in the circuit. The circuit used in this experiment, as as shown in the drawing above, is very simple and consists of two resistors in series. The two resistors were assumed to be equal in resistance.  Because of this, the voltage drop is the same between the teo two, which helped us predict that half of the voltage function of the circuit would be the voltage across the resistor

Apparatus:

The apparatus of this experiment consisted of the usual materials needed, such as a breadboard, two 100 ohm resistors, an analog discovery, a laptop with Waveforms software, a digital multimeter, wires and alligator clips. The different voltage functions were applied to the circuit using the Waveforms oscilloscope.

Procedure:

The schematic of this circuit, seen in the prelab above, was constructed using two 100 ohm resistors, the analog discovery box, and a breadboard. The different wave voltage functions were applied to the circuit using the yellow (W1) wires, and ground was placed on the other end of the circuit. It is not displayed in this picture, but the two orange wires (1+ and 1-) were placed across the resistor with the alligator clips.

Using the Waveforms software, the sinusoidal wave was created and then run into the circuit. The oscilloscope was then used to graph the voltage as a function of time across the circuit and the resistor with channel 1 across it. This is seen below:

As can be seen, the voltage function across the reistor (channel 1) is exactly half of the voltage across the circuit. Therefore, the frequency (1 kHz) and the period (1 ms) of each function is the same; however the only difference is the amplitude, where the amplitude for the resistor voltage function (1 V) is half the amplitude for the circuit voltage function (2 V). The same was also performed with a triangular wave, as shown below.

As can be seen, the period (1 ms) and the frequency (1 kHz) is the same for both voltage functions; however the only difference is the amplitude, where it is 1.5 V for the function across the resistor and 3 V across the circuit. Again, the function across the resistor is half the function of the circuit. The same was then done again for the square wave:

As expected the frequency (500 Hz) and the period (2 ms) is the same for both voltage functions. All that differs is the amplitude; the amplitude (2.5 V) of the circuit voltage is twice the amplitude (1.25 V) of the resistor voltage.

Data Analysis and Conclusion:

Above is the measured resistances of the resistor, along with the amplitudes and frequencies for each wave used.

As determined experimentally, the relationship between the voltage across the resistor and the whole circuit is linear; the voltage across the circuit is twice the voltage across the resistor, due to the resistance of the circuit being twice the resistance of the resistor under inspection.

Superposition II:

Purpose:

The purpose of this experiment is to find the voltage V across the 6.8 kohm resistor by using superposition for the 3 V and 5 V voltage sources. Then, the value of voltage obtained from the superposition theory was tested by building the circuit and then measuring the value using a voltmeter. The values were then also measured for removing the 3 V supply and then the 5 V supply from the circuit to see if superposition holds true.

Prelab:

The prelab of this experiment was to use the theory of superposition in electrical circuits to find the voltage V across the 6.8k ohm resistor. In the above picture, first the 3 V supply was not considered in the circuit, and the voltage across the resistor resulting from only the 5 V supply was found. Nodal voltage analysis was used to solve for this partial voltage.

The same was also done in that the other part of the partial voltage across the 6.8k ohm resistor was found resulting from solely the 3 V power supply. It was found that the voltage given by the 3 V supply is 1.99 V, and the voltage given by the 5 V supply was 0.71 V. Then, the total voltage across the 6.8k ohm resistor resulting from both supplies was found by adding the two partial voltages resulting from each isolated supply together. The true voltage across the 6.8k ohm resistor was then found to be 2.70 V.

To check this answer, the circuit was built in EveryCircuit, as seen below:

As seen above, the voltage across the 6.8k ohm resistor was found to be 2.70 V as well, showing that the theory of superposition does hold to be true.

Apparatus:

The apparatus of this experiment consisted of the same equipment used in the "Time-varying Signals" lab, with the exception of more resistors of varying resistances.

Procedure:

To see if superposition works in electrical circuits, the circuit seen in the Every Circuit schematic above was built using a breadboard, the analog discovery, resistors and wires, as seen below:

The 3 V power supply was provided using the Waveforms channel and the W1 wire. It was supplied to the 10k ohm resistor. The 5 V, given by the red wire, was provided to the 1k ohm resistor. The ground (seen by the yellow wire going out of the picture) was placed to the 22k ohm resistor, textbook to the schematic in the Every Circuit picture. The voltage across the 6.8k ohm resistor was then measured using a voltmeter (2.66 V).

The circuit was then slightly changed so that the 3 V supply is no longer part of the circuit, being replaced with a wire. Only the 5 V supply was left in the circuit. The voltage across the .8k ohm resistor in this set up was then measured (1.96 V). This set up is seen below.

The same was performed again, with the exception that the 3 V supply was left in the circuit and the 5 V supply was removed from the circuit. The voltage across the 6.8k ohm resistor was then measured (0.70 V). This is seen below:

Data Analysis and Conclusion:

The picture above shows the measured resistances of each of the resistors used. It also shows the voltages measured in the circuits with both voltage sources connected and only one connected in separate circuits. A table summing all of the useful data obtained is shown below:

The above table contains the experimental and calculated voltages across the 6.8k ohm resistor in circuits with the 5 V supply connected, the 3 V supply connected, and both the 5 V and 3 V supplies connected. It also contains the percent differences between the calculated and experimental voltages.

As can be seen, the percent differences are very small, which shows the the variations are due to assumptions (eg. no resistance in wires) and experimental uncertainties, such as measurement errors. Overall, it can be concluded that the superposition theory can be correctly applied to electrical circuits.