2/25/16: Day 2 - Resistors and Ohms Law - Voltage-Current Characteristics & Dependent Sources and MOSFETS

A lot was done on the second day of class. Many problems were solved and two experiments were performed. The day was started by solving another circuit teaser problem. Next, Ohm's law and resistance was reviewed. Conductance, the inverse of resistance, was also gone over. A problem involving finding the hot and cold resistance of a light bulb was then solved for.

Next, the lab titled "Resistors and Ohm's Law - Voltage-Current Characteristics" was performed. It is explained below in the labs section. After the lab the components of a circuit were reviewed. These include nodes, branches and loops. Their relationship with each other was also went over, and is known as the Fundamental Theorem of Network Topology. After, a problem involving identifying the number of loops, nodes and branches in a circuit was solved. Kircchoff's current and voltage laws were then reviewed from physics, and later the lab titled "Dependent Sources and MOSFETS" was performed.

LECTURE:

The above circuit teaser problem was first done. The question was what would the difference to the brightness of the light bulbs be, if any, if the switch was turned on from off, which is located on the wire between the two light bulbs. Because the batteries are the same, turning on the switch resulted in no change in voltage and current by Kirchhoff's laws. Because the current stayed the same, the power didn't change and the brightness stayed the same.

We then looked at the relationship between power and resistance using Ohm's law. It was found that the relationship is squared, or a quadratic, for both voltage and current.

This problem involved finding the hot and cold resistance of an incandescent light bulb. Finding the hot resistance was done using its power and the voltage difference across it. The cold resistance was then found using its resistivity constant rho for tungsten and the estimated length and cross-sectional area of the filament.

This problem involved finding the nodes, loops and branches of a certain circuit. The circuit had 7 branches; specifically, it has 5 resistors, a voltage supply and a current source. The circuit also has 5 nodes, which are splits in the flow of a wire. By the Fundamental Theorem of Network Topology, there must be three effective loops in the circuit, which are displayed in the picture.

In this problem, the current and voltage from points a to b were needed to be found based on the circuit's components. The direction of the 10 V and 8 V source was not given, so there were four different solutions depending on the directions. One solution was when both voltage sources were in the positive direction depending on the current. Another solution is when they were both in the negative direction. The last two solutions was when one was positive and the other negative. Knowing these circumstances Kirchhoff's voltage laws were used to find the current and voltage in the circuit.

LABS:

Resistors and Ohm's Law - Voltage-Current Characteristics:

Purpose:

The purpose of this experiment is to determine the resistance of a resistor by using Ohm's Law and finding the current running through the circuit for each voltage supplied. By Ohm's Law it is known that the resistance is linearly dependent on voltage by the current running through the resistor. The calculated resistance was then compared to the resistance measured by the ohmmeter. 

Apparatus:

The equipment of this experiment included a 100 ohm resistor, an analog voltage source and a laptop with Waveforms software, which was used to control the voltage source. A digital multimeter was also used as an ohmmeter, to measure the resistance of the resistor, a voltmeter, to measure the voltage in the circuit, and an ammeter, to measure the current through the circuit. Alligator clips were then used to connect the DMM to the circuit. The circuit was then set up on a breadboard, and wires were used to attach different components of the circuit together, as shown in the diagram below.

Procedure:

First, the resistance of the resistor was measured by using the digital multimeter as an ohmmeter. This setup is shown in the picture above. The resistance was measured to be 99.6 ohms.

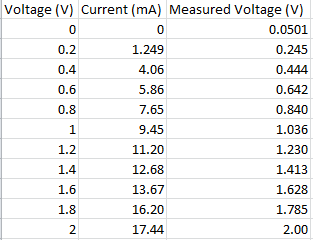
A circuit involving a digital multimeter as an ammeter, the 100 ohm resistor and the voltage supply (analog, powered by waveforms) connected in series was set up on the breadboard. The current, using the ammeter, was measured for 10 trials with voltages ranging from 0 to 2 V, with intervals of 0.2 V. For example, the first trial had 0 V, the second trial 0.2 V, the third trial 0.4 V, and so on. The multimeter was then disconnected from the circuit and placed in parallel to the resistor in order to measure the true voltage for each theoretically applied voltage. For example, a voltage of 0.245 V was measured for the theoretically applied voltage of 0.2 V.

The above picture represents the digital multimeter used as a voltmeter, connected to the circuit in parallel across the resistor. The wave wires attached to the analog voltage supply are connected to the circuit.

The above picture represents the digital multimeter being used as an ammeter, and being connected to the circuit in series. The wave wires attached to the analog voltage supply are connected to the circuit.

Above is the table that consists of the measured current and voltages applied to the circuit for each theoretical voltage. Using the data from this table, a graph of voltage vs. current was created, which is shown below.

Using Ohm's Law, which states that voltage is linearly proportional to current by resistance, it was found from the equation of the best fit curve that the resistance was experimentally calculated to be 112.8 ohms. The variable y is representative of voltage, and x is representative of current. The constant 112.78 is then the calculated resistance.

Conclusion:

The resistance of the resistor was calculated by Ohm's Law, and found to be 112.8 ohms. The actual measured resistance of the resistor using an ohmmeter was found to be 99.6 ohms. The largest reason why the experimental resistance is larger than the measured value is because the resistor, when used, becomes hotter due to converting electrical energy to thermal energy. Doing so raises the temperature of the resistor, and with a higher temperature comes an increase in the resistance. The experimental resistance is known as the "hot" resistance, whereas the measured resistance by the ohmmeter is known as the "cold" resistance.

On another note, it makes sense that a linear relationship was found between voltage and current because Ohm's Law states that they are linearly dependent. Neglecting the increase in resistance due to temperature increase and errors in uncertainty, it can be said that the Ohm's Law is valid for use in simple circuits like the one used in this experiment.


Dependent Sources and MOSFETS:

Purpose:

The purpose of this experiment was to experimentally determine the behavior of a MOSFET, a transistor as well as a voltage - controlled current source. An n-channel MOSFET was used, and its behavior was determined by obtaining the currents running through the circuits at specific applied voltages.

Apparatus:

The equipment of this experiment consisted of an analog discovery voltage source, which applied the desired voltage levels to the created circuit. A laptop with Waveforms was also needed to control the analog voltage source. A digital multimeter was also used as an ammeter, which measured the current running through the circuit at each applied voltage. A 100 ohm resistor was also used in the circuit along with the MOSFET. Lastly, a breadboard, alligator clips and wires were all used to connect all of the components of the circuit together.

Procedure:

The above circuit was constructed by placing the analog discovery, digital multimeter (ammeter), theoretical 100 ohm resistor, and the MOSFET in series. The 5 V wire (V+ - red) was attached to the drain of the MOSFET by first going to the ammeter and the resistor. The wave wire of the analog (W1 - yellow) was attached to the gate of the MOSFET, which is the middle of the three legs on the MOSFET. Lastly, the ground wire of then analog (black) was connected to the source of the MOSFET. This circuit was set up on a breadboard, as shown below:

Applying the desired voltage at the gate of the MOSFET using the Waveforms program allows current to run through the drain to the source. When voltage is applied to the drain the MOSFET is able to control the current of the circuit, depending on how much voltage is applied.

Voltages ranging from 0 V to 5 V were applied to the circuit, with each trial increasing with an increment of 0.3 V. The currents were recorded for each trial, and are shown below:

Data:

The MOSFET's threshold voltage, the voltage before which no current passes through the circuit, was found to be around 1.8 V. Based on this data, it is seen that the MOSFET acts as a voltage controlled current source. The current in the circuit is controlled by the MOSFET, and the value of the current depends on how much voltage is applied to the circuit.

Conclusion:

As can be seen in the graph above, before the threshold voltage (1.8 V) the MOSFET resists any current trying to run through the circuit. Once the voltage reaches past the threshold current is seen, which grows exponentially for a narrow range of voltage. After reaching past this narrow voltage range (1.8 - 2.7 V) the MOSFET only allows a maximum amount of current to flow through the system, and prevents any drastic changes to this current even if the voltage is increased.

The value of g of the circuit, which shows the linear relationship between the current and voltage through the MOSFET, was found by taking the trendline fir of the exponential portion of the graph (from 1.8 to 2.7 V). Based on the graph, the value of g for the circuit is found to be g = 0.0562.

Based on the data, it was confirmed that the MOSFET is a voltage-controlled current source. This is because the current in the MOSFET changes as a result of changing the voltage applied to the circuit. The MOSFET does not affect the voltage applied but only affects the resulting current based on the applied voltage.