MATLAB: Introduction to Numerical Computation

Purpose:

The purpose of this activity is to become more familiar with using MATLAB / FreeMAT for the purposes of this class' activities and problems. Simple math functions, matrices, and more complex linear equations were explored and solved in this experiment using FreeMAT.

Procedure:

The "Using FreeMAT as a Calculator" and "Redoing Errors" sections were completed in the above screenshot. The reason why sin(90) does not equal to 0 and sin(6.28) is negative in MATLAB is because MATLAB uses a radians mode, not a degree mode. 90 and 6.28 in MATLAB are processed as in radians even through the user wants them to be processed as in degrees.

"Assigning Expressions to Variables", "Creating an Array", "Automatically Creating Vectors" and "Transposing Arrays" section exercises were performed in the above screenshot.

"Applying Functions to Row Vectors" and "Array Operations" were completed in the above screenshots. As for the results, all of them made sense and no errors were received when the correct operations were used.

The exercises of "Addressing Arrays" and "Creating Simple Plots" sections were completed in the above two screenshots.

The above three pictures show completion of the exercise, in order, for "Adding Additional Plots to the Same Graph" section.

Exercise 1 of "Script Files" was completed in the above screenshot.

Above is the solution for Assignment 1 of "Solving Simultaneous Equations". It was found that the current through R3 is -0.1857 A.

Assignment 1 number 1 of "Plotting Exponentials" was completed in the above screenshot. It was found that as the time constant increases, the exponential curve changes less. For example, Circuit B, which has the largest time constant, corresponds to the green graph. Therefore, Circuit A will have the lowest output sooner.

This screenshot corresponds to number 2 of Assignment 1 of "Plotting Exponentials". Circuit A is represented by the blue graph, and circuit B is represented by the green graph.

Part 1 of Assignment 2 in the "Adding Sinusoids" section was answered in the screenshot above. It is seen that the actual output by FreeMAT is not equal to the theoretical output because FreeMAT read the phase angles in radians, and not in the desired degrees as the theoretical output did.

Part 2 of Assignment 2 for "Adding Sinusoids" is answered above.

Exercise 1a of "Complex Numbers" (there are two exercises marked as exercise 1 in this section).

Exercise 1b and 2 of "Complex Numbers".

Assignment 1 of "Complex Numbers"

Assignment 2 of "Complex Numbers"

Assignment 3 of "Complex Numbers"

Assignment 4 of "Complex Numbers"

Exercise 1 and Assignments 1 and 2 of "Solving for Roots of Equations"

Conclusion:

In this activity I learned simple math functions in FreeMAT, along with the basic use of the syntax of this program. I also learned how to make matrices in FreeMAT and how to add, multiply and transpose them. I also learned some basic formatting, writing functions in terms of variables and graphing those functions, even multiple functions on one graph. I also learned how to isolate parts of a matrix into its own array, and how to write script files and use them in FreeMAT. I learned how to solve circuit problems using matrices and how to work with complex numbers in FreeMAT. I learned how to convert from rectangular to polar coordinates and lastly how to solve LaPlace transforms by finding the roots of equations.

I can now say that I do know the basics of MATLAB that will be used for this class, and that MATLAB was not as difficult as I thought it would be, based on the experience with this activity.

2/25/16: Day 2 - Resistors and Ohms Law - Voltage-Current Characteristics & Dependent Sources and MOSFETS

A lot was done on the second day of class. Many problems were solved and two experiments were performed. The day was started by solving another circuit teaser problem. Next, Ohm's law and resistance was reviewed. Conductance, the inverse of resistance, was also gone over. A problem involving finding the hot and cold resistance of a light bulb was then solved for.

Next, the lab titled "Resistors and Ohm's Law - Voltage-Current Characteristics" was performed. It is explained below in the labs section. After the lab the components of a circuit were reviewed. These include nodes, branches and loops. Their relationship with each other was also went over, and is known as the Fundamental Theorem of Network Topology. After, a problem involving identifying the number of loops, nodes and branches in a circuit was solved. Kircchoff's current and voltage laws were then reviewed from physics, and later the lab titled "Dependent Sources and MOSFETS" was performed.

LECTURE:

The above circuit teaser problem was first done. The question was what would the difference to the brightness of the light bulbs be, if any, if the switch was turned on from off, which is located on the wire between the two light bulbs. Because the batteries are the same, turning on the switch resulted in no change in voltage and current by Kirchhoff's laws. Because the current stayed the same, the power didn't change and the brightness stayed the same.

We then looked at the relationship between power and resistance using Ohm's law. It was found that the relationship is squared, or a quadratic, for both voltage and current.

This problem involved finding the hot and cold resistance of an incandescent light bulb. Finding the hot resistance was done using its power and the voltage difference across it. The cold resistance was then found using its resistivity constant rho for tungsten and the estimated length and cross-sectional area of the filament.

This problem involved finding the nodes, loops and branches of a certain circuit. The circuit had 7 branches; specifically, it has 5 resistors, a voltage supply and a current source. The circuit also has 5 nodes, which are splits in the flow of a wire. By the Fundamental Theorem of Network Topology, there must be three effective loops in the circuit, which are displayed in the picture.

In this problem, the current and voltage from points a to b were needed to be found based on the circuit's components. The direction of the 10 V and 8 V source was not given, so there were four different solutions depending on the directions. One solution was when both voltage sources were in the positive direction depending on the current. Another solution is when they were both in the negative direction. The last two solutions was when one was positive and the other negative. Knowing these circumstances Kirchhoff's voltage laws were used to find the current and voltage in the circuit.

LABS:

Resistors and Ohm's Law - Voltage-Current Characteristics:

Purpose:

The purpose of this experiment is to determine the resistance of a resistor by using Ohm's Law and finding the current running through the circuit for each voltage supplied. By Ohm's Law it is known that the resistance is linearly dependent on voltage by the current running through the resistor. The calculated resistance was then compared to the resistance measured by the ohmmeter. 

Apparatus:

The equipment of this experiment included a 100 ohm resistor, an analog voltage source and a laptop with Waveforms software, which was used to control the voltage source. A digital multimeter was also used as an ohmmeter, to measure the resistance of the resistor, a voltmeter, to measure the voltage in the circuit, and an ammeter, to measure the current through the circuit. Alligator clips were then used to connect the DMM to the circuit. The circuit was then set up on a breadboard, and wires were used to attach different components of the circuit together, as shown in the diagram below.

Procedure:

First, the resistance of the resistor was measured by using the digital multimeter as an ohmmeter. This setup is shown in the picture above. The resistance was measured to be 99.6 ohms.

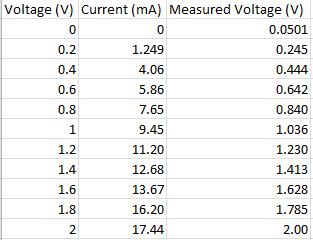
A circuit involving a digital multimeter as an ammeter, the 100 ohm resistor and the voltage supply (analog, powered by waveforms) connected in series was set up on the breadboard. The current, using the ammeter, was measured for 10 trials with voltages ranging from 0 to 2 V, with intervals of 0.2 V. For example, the first trial had 0 V, the second trial 0.2 V, the third trial 0.4 V, and so on. The multimeter was then disconnected from the circuit and placed in parallel to the resistor in order to measure the true voltage for each theoretically applied voltage. For example, a voltage of 0.245 V was measured for the theoretically applied voltage of 0.2 V.

The above picture represents the digital multimeter used as a voltmeter, connected to the circuit in parallel across the resistor. The wave wires attached to the analog voltage supply are connected to the circuit.

The above picture represents the digital multimeter being used as an ammeter, and being connected to the circuit in series. The wave wires attached to the analog voltage supply are connected to the circuit.

Above is the table that consists of the measured current and voltages applied to the circuit for each theoretical voltage. Using the data from this table, a graph of voltage vs. current was created, which is shown below.

Using Ohm's Law, which states that voltage is linearly proportional to current by resistance, it was found from the equation of the best fit curve that the resistance was experimentally calculated to be 112.8 ohms. The variable y is representative of voltage, and x is representative of current. The constant 112.78 is then the calculated resistance.

Conclusion:

The resistance of the resistor was calculated by Ohm's Law, and found to be 112.8 ohms. The actual measured resistance of the resistor using an ohmmeter was found to be 99.6 ohms. The largest reason why the experimental resistance is larger than the measured value is because the resistor, when used, becomes hotter due to converting electrical energy to thermal energy. Doing so raises the temperature of the resistor, and with a higher temperature comes an increase in the resistance. The experimental resistance is known as the "hot" resistance, whereas the measured resistance by the ohmmeter is known as the "cold" resistance.

On another note, it makes sense that a linear relationship was found between voltage and current because Ohm's Law states that they are linearly dependent. Neglecting the increase in resistance due to temperature increase and errors in uncertainty, it can be said that the Ohm's Law is valid for use in simple circuits like the one used in this experiment.


Dependent Sources and MOSFETS:

Purpose:

The purpose of this experiment was to experimentally determine the behavior of a MOSFET, a transistor as well as a voltage - controlled current source. An n-channel MOSFET was used, and its behavior was determined by obtaining the currents running through the circuits at specific applied voltages.

Apparatus:

The equipment of this experiment consisted of an analog discovery voltage source, which applied the desired voltage levels to the created circuit. A laptop with Waveforms was also needed to control the analog voltage source. A digital multimeter was also used as an ammeter, which measured the current running through the circuit at each applied voltage. A 100 ohm resistor was also used in the circuit along with the MOSFET. Lastly, a breadboard, alligator clips and wires were all used to connect all of the components of the circuit together.

Procedure:

The above circuit was constructed by placing the analog discovery, digital multimeter (ammeter), theoretical 100 ohm resistor, and the MOSFET in series. The 5 V wire (V+ - red) was attached to the drain of the MOSFET by first going to the ammeter and the resistor. The wave wire of the analog (W1 - yellow) was attached to the gate of the MOSFET, which is the middle of the three legs on the MOSFET. Lastly, the ground wire of then analog (black) was connected to the source of the MOSFET. This circuit was set up on a breadboard, as shown below:

Applying the desired voltage at the gate of the MOSFET using the Waveforms program allows current to run through the drain to the source. When voltage is applied to the drain the MOSFET is able to control the current of the circuit, depending on how much voltage is applied.

Voltages ranging from 0 V to 5 V were applied to the circuit, with each trial increasing with an increment of 0.3 V. The currents were recorded for each trial, and are shown below:

Data:

The MOSFET's threshold voltage, the voltage before which no current passes through the circuit, was found to be around 1.8 V. Based on this data, it is seen that the MOSFET acts as a voltage controlled current source. The current in the circuit is controlled by the MOSFET, and the value of the current depends on how much voltage is applied to the circuit.

Conclusion:

As can be seen in the graph above, before the threshold voltage (1.8 V) the MOSFET resists any current trying to run through the circuit. Once the voltage reaches past the threshold current is seen, which grows exponentially for a narrow range of voltage. After reaching past this narrow voltage range (1.8 - 2.7 V) the MOSFET only allows a maximum amount of current to flow through the system, and prevents any drastic changes to this current even if the voltage is increased.

The value of g of the circuit, which shows the linear relationship between the current and voltage through the MOSFET, was found by taking the trendline fir of the exponential portion of the graph (from 1.8 to 2.7 V). Based on the graph, the value of g for the circuit is found to be g = 0.0562.

Based on the data, it was confirmed that the MOSFET is a voltage-controlled current source. This is because the current in the MOSFET changes as a result of changing the voltage applied to the circuit. The MOSFET does not affect the voltage applied but only affects the resulting current based on the applied voltage.

2/23/16 Day 1: Solderless Breadboards, Open-circuits and Short-circuits

LECTURE:

In lecture today the day was started with a teaser problem involving lights and circuits. Then charge and current were reviewed and a problem was solved about the relationship between the two. Then, voltage, power and energy was also reviewed from physics 4B and a problem relating all of these concepts together was solved. The Solderless Breadboards lab was then performed, and its review is found below under the lab section. After the lab power and energy was dived into more detail, and a problem solving for energy and power from voltage and current was solved. An overview of dependent and independent power sources, what they are and how they are indicated and used was reviewed after the problem, and then a problem concerning conservation of energy in a circuit was solved to find the voltage across an object in the circuit.

Found above is the teaser problem. It consisted of a circuit with two voltage sources and three light bulbs. As seen above, there is a light bulb found between the sources with a switch next to it, Initially the center light bulb is off because the switch is off (there is no connection to the sources). The upper and lower light bulb were one at a certain brightness. A hypothesis had to be performed about all three light bulbs after the switch was turned on. It was found that the two light bulbs previously turned on stayed at the same brightness whereas the center bulb stayed off after the switch was turned on. The two light bulbs stayed the same because the current running through them and the voltages across them was the same even after turning on the switch. The center bulb stayed off because there was no potential difference across it, and therefore no current was running through it.

In this problem, a graph of charge as a function of time was given, and current as a function of time was asked to be found. By knowing that i(t) = dq/dt, the current was easily found by first finding the formula for charge and then taking the derivative. The graph is a sinusoidal graph that begins at 0 at the origin, so it is know that charge is a sin function. The period was found to be pi s, so therefore the angular frequency was found to be 2 rad/s. Using the general form q = q(max) sin (wt), the formula for charge was found, and taking the derivative the current as a function of time was obtained.

In this problem i(t) was given and total charge in 2 seconds was wanted to be found. Knowing that q is the integral of i times dt, the charge function was found. With the limits from 0 < t < 2, the charge obtained in 2 sec was found.

It this problem voltage and a graph of current as a function of time was given. The problem asked for power and energy as a function of time. Multiplying the graph of i(t) by V, the graph of power as a function of time was found. Then, integrating P(t) allowed for finding the graph of energy as a function of time. From 0 < t < 2, the integral of a constant is a linear graph. Same goes from 2 < t < 4. From 4 < t < 6, the integral of 0 is just 0.

Graphs of current and voltage as functions of time was provided in this problem. The problem asked for finding the graph of power and energy, as well as finding the total energy from 0 < t < 4 seconds, the period. Piece-wise functions of i(t) and v(t) were found, and multiplying them together gave power as a function of time in a piece-wise function. Using the function the graph of P(t) was drawn. Then integrating P using dt intervals was done to find the piece-wise function of energy, and then E(t) was graphed. Then, the total energy in a period was found was integrating P * dt from 0 < t < 4 seconds.

The previous circuit was given, and the voltage Vo of the part of the circuit in the middle of the diamond shape.Using the conservation of energy principle, it was found that the power provided is equal to the power used in a circuit. Using these principles, the voltage Vo was found to be 20 volts.

LAB:

Purpose:


The purpose of this experiment was to experimentally determine the circuit layout of a breadboard, and how the holes in rows and columns are connected and whether the connections form open or closed circuits. Another purpose of this experiment was to learn how to use a digital multimeter to measure the resistance of a circuit.


Apparatus:

The materials used in this experiment include a digital multimeter (as an ohmmeter), alligator clips, jumper wires and a breadboard. The digital multimeter was used to measure the resistance of different wires and circuits. The jumper wires and alligator clips were used to attach the ohmmeter to the breadboard to measure its resistance. The breadboard was used to study its internal circuits and how the holes in the rows and columns are connected to form open and short circuits.


Procedure:

First, the leads of the ohmmeter were attached to holes in the breadboard that were in the same row on one side. The leads were attached to the holes in columns f and j on row 57. The ohmmeter measured a small resistance of  1.6 Ω.

Next, the leads of the ohmmeter were connected to holes in the breadboard that were in the same row but on different sides of the breadboard. The leads were connected to holes in columns a and j of row 57. An immeasurable resistance was picked up by the ohmmeter.

Then, one of the leads of the ohmmeter was disconnected and reattached to a hole in the breadboard that was on a different row and column on different sides. The leads were placed on rows 50 and 57 in columns j and a, respectively. Again, the ohmmeter measured a very large resistance, as shown in the picture above.

Lastly, the leads were left in the same position as before (one in row 57 column j and the other in row 50 column a). However, a jumper wire was used to connect the two rows (nodes) together. The resistance turned to be small again, measured by the ohmmeter as 2.7 Ω.




Data Analysis:

The resistances measured by the ohmmeter for the first and last procedures were low, whereas the resistances for the middle two procedures were immeasurable by the ohmmeter. Because of this, it shows that the first and last procedures (situations 1 and 4) consisted of connections between the holes. These connections correspond to "short circuits" or "closed circuits", where all of the wires are connected to form a circuit loop. On the other hand, the middle two procedures (situations 2 and 3) had no connections for the circuits, indicated by the infinite resistance. These disconnections show that the circuits in situations 2 and 3 were "open circuits", where there is a disconnection in the circuit, not allowing the electrons to flow and cause a current if the circuit were attached to a voltage supply.


Conclusion:

The connections layout of a breadboard and the use of a digital multimeter as an ohmmeter were determined in this experiment. The connections of a breadboard consist of all the holes in each row on one side connected to each other, as shown in the top figure. Also, the holes of two columns on each side of the breadboard are also connected vertically, as seen in the above picture. This layout of the breadboard was determined by connecting the leads of the digital multimeter to different holes in either same rows and/or columns or different rows and/or columns, as explained in the four steps of the procedure above. The resistances read by the ohmmeter was also used in order to determine whether the way the ohmmeter was connected resulted in an open or closed circuit. An infinite resistance was found to imply an open circuit, and a very small resistance was found to imply a closed circuit.