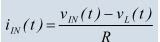Day 30 6/2/16: Series and Parallel Resonance Circuits, and Passive Filters

LECTURE:

In the above derivation, the half-power frequencies were determined. These frequencies are the frequencies where the dissipated power is half the maximum, or where the rms voltage/current is obtained. The graphs of frequency versus voltage/current are bell-shaped, so there are actually two frequencies where the dissipated power is halved, which is given by the derived formulas above (the results of a quadratic). The distance between the two half-power frequencies is termed the bandwidth.

In this example, the objective was to determine the resonant frequency and half-power frequency of this series RLC circuit. The resonant frequency for any RLC circuit is given by 1 over root LC. Then, the half-power frequencies were found using the derived formulas above. Next, the bandwidth and quality factor were determined. The bandwidth was given as the difference between the upper and lower half-power frequencies. The quality factor is given as the quotient between the resonant frequency and the bandwidth. Lastly, the amplitude of the current at the resonant and two half-power frequencies was determined. This was found by dividing the voltage by the impedance. At the resonance frequency there is only resistor and no reactance. At the half-power frequencies the current is just the rms of the amplitude of the current.

In this problem, the objective was to find the resonant frequency, quality factor and the bandwidth of the parallel RLC circuit. The resonant frequency, as always, is given by 1 over the root of LC. The bandwidth is given as the difference between the upper and lower half-power frequencies, or the resonant frequency divided by the quality factor since it is greater than 10. Next, the quality factor is given by multiplying the resonant frequency by RC. 

In this example, the inductance and capacitance needed to obtain a bandwidth of 5 kHz and a resonant frequency of 640 kHz for the above series RLC circuit was determined. The resistance was given as 10 kOhms. The inductance was found by dividing the resistance by the bandwidth, and the capacitance was found from the resonant frequency using the recently determined inductance.

In this example, the cutoff frequency of the above filter was determined. The transfer function was first obtained, and then the transfer function values at time 0 and time infinity were calculated. Since the transfer function of time 0 is 1 and the transfer function at time infinity is zero, it was deduced that the filter is low pass.

Summary:

No lab was done this lecture meeting. Resonance in series and parallel RLC circuits were determined. This included the resonant frequency, half-power frequencies, bandwidth, quality factors and transfer functions. Then, the four different passive filters were reviewed. These were the high pass, low pass, bandpass, and bandstop filters. The low pass filter is given by and RC circuit, with the capacitor providing the output voltage. A lowpass filter has a 1 transfer function at time 0 and a zero transfer function at infinite time. A highpass filter also consists of an RC circuit, but the resistor is the output voltage provider. A highpass filter has a transfer function of zero at time 0 and a transfer function of 1 at infinite time. Next, a bandpass filter consists of a series RLC circuit, with the resistor as the output voltage provider. The bandpass filter is given a transfer function of 1 in the bandwidth region, and zero everywhere else. Lastly the bandstop filter is the opposite of the bandpass; it has a transfer function of zero in the bandwidth and 1 everywhere else. It also consists of a series RLC circuit, but the output voltage is the inductor and capacitor. 

Day 28; 26 May 2016: Transfer Functions, Frequency Responses, and Signals with Multiple Frequency Components

We first learned about the frequency response, which provides information about the behavior of a circuit as a function of the frequency of the source provided. We then learned about transfer functions, which provides the frequency response of a circuit when they are plotted. The transfer function is frequency-dependent and given by the ratio of a phasor output to a phasor input. The tranfer function can be given by voltage gain, current gain, transfer impedance (v/i) and transfer admittance (i/v). We then did many problems for calculating the transfer function and using it to graph the frequency response.

Next, the decibel and logarithmic scales were reviewed. In logarithmic scale, it was found that the gain with respect to voltage or current is 20log(V2/V1) - 10log(R2/R1). When R1 = R2, it simplifies to 20log(V2/V1). Lastly, we did a lab titled "Signals with Multiple Frequency Components".

LECTURE:

In this example, the current gain of the circuit was calculated. The capacitor was assumed to be the output of this circuit. Using current divider, the current across the capacitor was found, then divided by the total input current to obtain the transfer function as current gain. The zeros were then found by setting the numerator equal to zero, and the poles were found by setting the denominator to zero.

The purpose of this problem was to find the transfer impedance of this circuit and to sketch the frequency response. Using nodal analysis the transfer function Vo/I was determined, where the output voltage is the voltage across the inductor. This transfer function was then used to graph the frequency response in MATLAB. This is shown below:

The code used to graph in MATLAB is shown below:

In the problem below, the transfer function as a voltage gain was determined using simple KVL, where the output voltage was the voltage across the inductor. The values of jw when the gain beta is zero was determined, along with the values at an infinite beta.

LAB:

Signals with Multiple Frequency Components:

Purpose:

The purpose of this lab was to find the frequency response of an electrical circuit and determine the effect of the circuit on input signals such as multiple sinusoidal waves of different frequencies in one input and a sinusoidal signal with a time-varying frequency as another input.The experimental response of the circuit to these input signals was then measured and compared to the expected. In addition,  a circuit’s effect on the “shape” of a signal applied via the response was determined.

Prelab:

The parallel RC circuit shown in the picture above was analyzed by determining the transfer function (voltage gain) at different frequencies. The output voltage was the voltage across the parallel resistor with the capacitor. 

Apparatus:

The apparatus was the circuit seen in the prelab, along with the analog discovery and the laptop with Waveforms software.

Procedure/Data:

First, the circuit above was constructed. Channel 1 was used to measure in input voltage and Channel 2 to measure the output voltage, or the voltage across the resistor in parallel with the capacitor. The waveform generator was then used to apply the following wave equation: 

20[sin(1000pi*t) + sin(2000pi*t) + sin(20,000pi*t)

The output and input voltages were then measured in the oscilloscope window, which is shown below.

Below is another sine function that was applied to the circuit. It involves a sinusoidal wave of equal frequency but constantly changing amplitudes. 

Lastly, a sinusoidal sweep was applied to the circuit. A sinusoidal sweep in a sine wave whose frequency increases with time, as shown below. The amplitudes also varies with each period and slightly throughout one period. The oscilloscope window is shown below:

Data Analysis:

Based on all three oscilloscope graphs obtained, it seemed that the circuit greatly reduced the noise in the input and made all of those weird sinusoidal inputs more like traditional sinusoidal waves with fairly constant amplitude and frequency, except for the sinusoidal sweep. Overall, though, the output has really been a very unintensified version of each input, making it more like a traditional sine wave. This data obtained is expected based on the results obtained from the prelab and the calculations seen above. As the frequency increases, the voltage gain decreases, which was seen in these oscilloscope windows, especially the sinudoidal sweep.

Day 27 5/24/16: RMS Values, Average and Apparent Power, Power Factor, Complex Power, and Power Factor Correction

First of all, we went over what an rms value is and how to determine the rms value of different sinusoidal signals. The rms value in circuits is the equivalent dc source compared to the ac source that would provide the equivalent average power. We then did a problem of finding the rms value for a sinusoidal time-varying signal.
Next, we reviewed apparent power, average power and the power factor. Apparent power, denoted as S, is the product of the rms values of the voltage and current, or 1/2 times the maximum voltage and current. This is so because the rms values of voltage and current are max voltage/current divided by the square root of 2. Moving on, the average power is the apparent power times the power factor, or the cosine of the difference between the phase angle of voltage and current. The power factor is also the cosine of the angle of the load impedance. We then did a problem involving these different powers.
After, we learned about complex power, which is given by multiplying half of the voltage by the complex conjugate of the current. It is also given by multiplying the apparent power by the sine of the phase difference between voltage and current. The apparent power is given by the average power plus j times the complex power.
We then learned about the power triangle, which provides the apparent power (hypotenuse), the average power (leg on x-axis), complex power (leg parallel to y-axis) and the power angle. When the triangle is in the 4th quadrant, the load is capacitive and therefore the pf is leading. When the triangle is in the 1st quadrant, the load is inductive and therefore the pf is lagging. We then did a problem involving the power triangle.
Next, we learned about power factor correction in that the power factor can be increased simply by installing a capacitor in parallel to an inductive load, since purely inductive loads operate at low pf. A problem was then solved involving power factor correction. We then did a lab titled "Apparent Power and Power Factor Correction".

LECTURE:

Above is the derivation for the rms value for current. All other rms values follow the same equation, with the fact that a value other than current is replaced with the current in this equation.

In this problem, the objective was to determine the rms value for this sinusoidal wave. The formula for rms was used in this problem, with the value in the formula being the equation of this time-varying signal, or 2Vp*sin^2(wt). The rms value was found to be the square root of 1.5 times Vp.

In the above picture, we came up with an acronym to remember the phase angles of voltage and current for inductors and capacitors. This acronym is Eli the Iceman. Eli tells use that the inductor's voltage (emf) leads the current by pi/2. Ice tells us that the voltage (emf) of the capacitor lags the current by pi/2.

In this example, the apparent and average power of the load (30 ohm resistor and 0.5 H inductor) were determined, along with the power factor.

In this example, using the provided voltages and currents the apparent power, average power, complex power, power factor and impedance was determined. These values were then plotted on a power triangle. Because the power triangle is in quadrant iv instead of i, it indicates that the load is capacitive (or a leading pf).   

In this problem, the necessary capacitance was determined in order to bring the power factor from 0.8 up to 0.95. First, the difference in complex power before and after the power factor correction was determined, then it was divided by the frequency and the rms voltage squared to determine to need a capacitance of 310 uF to bring up the power factor from 0.8 to 0.95. 

LAB:

Apparent Power and Power Factor Correction:

Purpose:

The purpose of this experiment was to analyze apparent power and power factor of a load and to determine the effects of changing the resistance of the load on the apparent power, average power and power factor. The load is connected to a resistive network. Expectations were determined and those were tested on a real circuit and via measurements. It was expected that a larger difference between apparent and average power correlated to a small power factor and that the power provided to the load would be much less.
Prelab:

In the prelab, different values were determined at different resistances for the load. The inductive reactance, however, stayed the same, along with the transmission resistance. In the prelab, the RMS current delivered by the source, the RMS load voltage, the average power delivered to the load, the apparent power delivered to the load, the load's power factor, the average power dissipated in the transmission resistor and the ratio between the average power dissipated in the transmission resistor and the average power delivered to the load were determined. 

Procedure/Data:

First, the circuit seen in the prelab was first constructed, as seen above. In this picture, the 10 ohm resistor is placed in the load impedance. A wavegen channel was used to aply the input voltage. Channel 1 was used to measure the input voltage and channel 2 was used to measure the voltage across the load. The oscilloscope window was then used to determine the input voltage and voltage across the load. A math function ws also created to determine the current through the circuit. This oscilooscope window for the 10 ohm load resistor is shown below.

The same was then done with a 47 ohm load resistor instead of a 10 ohm load resistor. The reactance of the inductor stayed constant throughout the whole experiment.Below is the circuit with the 47 ohm load resistor.

Again, Ch1 was used to measure input voltage and Ch2 was used to measure the load voltage. The oscilloscope window is shown below along with a math channel to read current.

Again, the same setup and procedure was done again, with the exception that now a 100 ohm load resistor was used in replacement with the 47 ohm load resistor. The circuit is shown below.

Below is the oscilloscope window for this circuit. The same channels were used as prior.

The oscilloscope windows were then used to determine the data obtained and needed from this experiment. This data is the same as that calculated in the prelab. This data is shown in the data analysis section below.

Data Analysis / Conclusion:

Above is the data obtained from the oscilloscope windows measured in the procedure and displayed in the data section. What's inside the table is the expected results, and what's outside is the obtained data from the experiment. Looking at the 10 ohm load resistor, the experimental load voltage (840 mV) is larger than the theoretical (626 mV), with a percent difference of 34.2%. It is unknown exactly why this might have occurred, but it is possible that because small impedances were used, any small change in the resistance or reactance resulted in a larger change in voltage and current. Agsain, the current is the same; a percent difference of 36.8% between the expected (19 mA) and the experimental (26 mA). This also applies to the other trials involving the 47 ohm and 100 ohm load resistors, which helps verify that it is most likely due to the inductor not being 1 mH but actually deviating from it. Since the inductance is very small, the change affected the results dramatically.

Below is the experimental power factor, apparent power, average power, power dissipated by the transmission resistor, and the ratio between the transmission power and load power.

As can be seen, with an increasing load resistor, the power factor increases along with the ratio between transmission power and load power. However, the apparent power decreases with increasing load resistance. An interesting note is that the average power for both the load and transmission is largest when the load resistance is at 47 ohms.

5/19/16 Day 26: Op Amp AC Circuits, Oscillators, Instantaneous and Average Power and Max Power Transfer

We first quickly reviewed how to solve for op amp ac circuits, which involve nodal analysis and complex algebra. We the did a problem involving ac in op amp circuits. We then learned about oscillators, which convert dc inputs to ac outputs. This is done by using an op amp circuit with a gain of one or greater and by resulting in no phase shift between input and output. Another interesting part of oscillators is that their op amp has two feedbacks and not just one. We then reviewed a Wein-bridge oscillator, the simplest oscillator. After, we did a lab on the op amp relaxation oscillator. Lastly, we went over average and instantaneous power. Average power was found to be 1/2VIcos(v-i), where v and i are phase shifts for the voltage and current, respectively. We then did a problem involving power. Lastly, we quickly reviewed max power transfer for ac circuits, which occurs when the load impedance is the complex conjugate of the Thevenin impedance. The max power is also given by (V_th)^2/(8R_th).  

LECTURE:

In this example, the output voltage of this op amp ac circuit was determined. As in all op amp circuits, nodal analysis was used. The exception in this case is that impedances and time-varying voltages were taken into account. The answer was determined to be 1.029cos(1000t+59.04) V.

In this derivation above, the simplest Wein-bridge oscillator was solved for. It was found that for the resistance to be equal to the capacitance, the gain of such an oscillator is three and its angular velocity is 1/3. For such an oscillator, there is no imaginary part, only real values.

In this problem, the objective was to determine the average power each circuit element absorbs. Right off the bat we can tell that the average power absorbed by the capacitor and inductor are zero, since only resistors absorb an average power; capacitors and resistors absorb and release and equal amount of power, making the average zero. Then, the voltages and currents across each resistor were determined, and by this, the power was found. It was found that the source supplies 7.5 W of power, the 4 ohm resistor absorbs 5 W, and the two ohm resistor absorbs 2.5 W. This is expected, since the sum of the power in the circuit must be zero.

LAB:

Op Amp Relaxation Oscillator:

Purpose:

The purpose of this experiment was to generate a relaxation oscillator and to analyze its output behavior. A relaxation oscillator that would generate oscillations close to the expected (given from EveryCircuit) was also another goal of this lab.

Prelab:

The purpose of the prelab was to determine the resistance value of inverting feedback resistor needed to generate a frequency of 159 Hz in the relaxation oscillator. The other two parallel resistors were assumed to be equal. Beta was found to be a half and from this the resistance was determined from the period function T = 2 R C ln ((1+beta)/(1-beta)). 

Then, the determined resistance (2.86 kOhm) was tested using EveryCircuit by determining the resulting frequency of adding that value of resistance. Based on EveryCircuit, the frequency was found to be 158 Hz using such a resistance, which is very close to the needed value of 159 Hz.

Procedure:

The circuit was put to the test by first building it, as seen above. The schematic of this circuit is seen in the prelab above. For the two parallel resistors, a value of 1 kOhm was used. In addition, a 1 uF capacitor was also used. Then, using Waveforms, the output voltage and the voltage across the capacitor were measured on the oscilloscope window. The windows are shown below in the data section. Also, a 3 kOhm resistor was used instead of 2.86 kOhm, since that was the closest resistance value available.

Data:

Above is the oscilloscope window for the voltages as functions of time across the capacitor and the output voltage. The yellow graph is the voltage across the capacitor, and the blue is the output. As can be seen, the op amp goes repeatedly through positive and negative saturation, creating a square wave. In addition, comparing this window to the obtained graph in EveryCircuit, they are very similar, which shows that the procedure was performed correctly.

Data Analysis / Conclusion:

Based on this window, the frequency was experimentally calculated. The calculation is shown below: 

 As can be seen, the experimental frequency (163.7 Hz) was close to the expected (159 Hz), which shows that the method used to analyze oscillators is correct. There is a percent difference of 2.96%, and most, if not all, of this small difference is due to using a 3 kOhm resistor instead of a 2.85 kOhm.

5/17/16 Day 25: Sinusoidal Steady State Analysis in AC Circuits and Phasors: Passive RL Circuit Response

In class we learned how to apply all of the previously learned circuit analysis techniques to AC circuits instead of DC circuits. We learned how to apply nodal analysis to AC circuits, which is very similar to DC with the exception that impedance is used instead, and that everything is done in complex form, which requires complex algebra. A problem involving nodal analysis was then performed. We then learned about mesh analysis, which is exactly like mesh analysis in dc with similar exceptions as in nodal analysis. A problem involving mesh analysis in ac was then performed. After, we did a lab titled "Phasors: Passive RL Circuit Response".

Next, we reviewed superposition in ac circuits. It is very similar to superposition in dc, with the exception that impedance is used and therefore complex algebra, as in the other analysis techniques in ac. Lastly, source transformations and Thevenin and Norton equivalents were also reviewed, which involve the same concepts as in dc but the same exceptions as in the other analysis techniques in ac.

LECTURE:

In this problem, nodal analysis was used in ac circuits to find the current across the 0.1 uF capacitor. There are only two viable voltage nodes, which were used for the analysis.

In this problem, the objective was to find the current across the 4 ohm resistor. This was achieved using mesh current analysis, and again, because we are in ac, more complex algebra was seen.

In this problem, superposition principle was used to find the current across the 4 ohm resistor. As can be seen, this is the same circuit that was analyzed in the previous example. The same circuit was used to verify that superposition principle and mesh analysis can be used in ac circuits correctly. The same conditions apply for superposition in ac as in dc; current sources act as open circuits and voltage sources act as short circuits.

In this simple problem, source transformations were practiced in simple ac circuit analysis. They ae performed the same exact way as in dc circuit analysis, with the exception that now complex algebra must be used.

The Thevenin equivalent of this circuit was determined using Thevenin's Theorem and impedance equivalents. The pair of impedances in series were added to obtain equivalent impedances, and then KCL and KVL was performed to solve for the Thevenin voltage and Thevenin impedance.

LAB:

Purpose:

The purpose of this experiment was to analyze the steady-state response of an RL circuit with AC signals applied. The frequency was the same throughout the entire circuit, but each component had a different phase angle and amplitude. Because they are all at the same frequency as well, the amplitude gain between the input and output could be determined. The experimental values were confirmed by comparing to theoretical values solved for in the prelab.

Prelab:

In the prelab, the amplitude gain and phase difference were derived for an RL circuit. Then the cutoff frequency of this circuit was solved for with the given resistance and capacitance values. The cutoff frequency is R/L for an RL circuit. Next, the amplitude gain and phase difference at a tenth of the cutoff frequency, at the cutoff frequency, and at ten times the cutoff frequency were calculated. Then, the behavior of the inductor at those frequencies was predicted and used to prove the calculated amplitude gain. At low frequencies, the inductor acts close to a wire, providing a very large amplitude gain. On the other hand, at high frequencies, the inductor acts close to an open cicuit, providing a very small amplitude gain.

Apparatus:

The equipment of this experiment included: a breadboard, an inductor, a resistor, wires, an analog discovery and a laptop with Waveforms.

Procedure:

First, the RL circuit, consisting of a 47 ohm resistor in series with a 1 mH inductor, was created. Then, the wavegen on waveforms was used to apply a sinusoidal input of 2 V at the frequencies given by a  tenth of the cutoff frequency, the cutoff frequency itself, and ten times the cutoff frequency. Channel 1 was used to measure the input voltage, and channel two of the oscilloscope was used to measure the voltage across the inductor. Then, a math channel was used to determine the current through the circuit. The formula is shown below:

Below is the oscilloscope window for a tenth of the cutoff frequency:

As can be seen, the voltage across the inductor is very small, which shows that it acts close to a wire under low frequencies. The oscilloscope window for the cutoff frequency is shown below:

Lastly, the oscilloscope window for 10 times the cutoff frequency is shown below:

As can be seen, the voltage across the inductor is roughly equal to the input voltage, which shows that at high frequencies it acts like an open circuit, eating up almost all of the voltage provided.

All of the data obtained form analyzing the windows is shown in data below:

Data:

Above is the data obtained from the oscilloscope windows. Again, it is expected that the voltage drop across the inductor at low frequencies is small, because the inductor acts close to a wire. At high frequencies, it is expected that the inductor eats up nearly all of the voltage applied, since it acts as an open circuit at high frequencies. Therefore, it is also expected that the current is very small at these high frequencies.

Data Analysis/Conclusion:

Analyzing the data obtained to the calculations in the prelab, all of the obtained data is very close to the calculated values, which shows that the circuit analysis used in this experiment is correct. It is expected that the gain at low frequency is the largest and the gain at high frequency is the smallest, since at low frequencies the inductor acts as a wire and at high frequencies the inductor acts as an open circuit. In addition, the phase shifts obtained experimentally are very close to the determined values, which shows that the analysis is correct. Unfortunately, there is no conceptual way to determine the phase shift at the frequencies as there is for the gain and current.